第3章遅延学習 - 最近傍法を使った分類

R Packages
3.1 最近傍法による分類とは何か【P60】
3.2 実例 - k近傍法を使った乳ガン診断【P68】
3.3 まとめ【P78】
Case Study 【テキスト外】
参考資料

第三章で学ぶ分類を目的とした教師あり学習アルゴリズムの最近傍法で、多変量（フィーチャー）なデータや多水準（クラス）なデータを分類するのに適したアルゴリズムです。

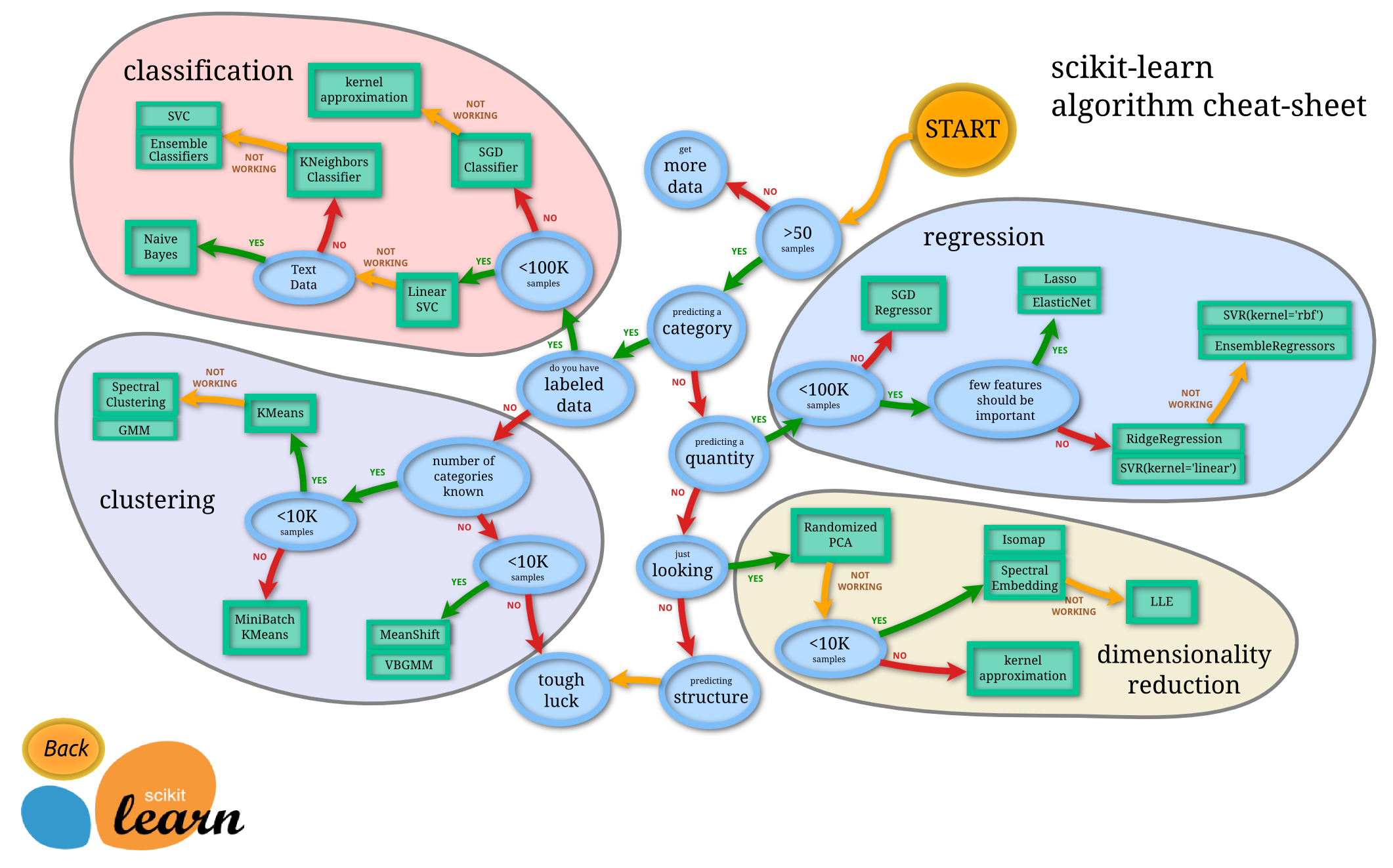
scikit-learn algorithm cheat-sheet

　
同一の水準（クラス）のデータ（インスタンス）ならば、変量（フィーチャー）も同質の傾向になるという前提で分類（ラベル付け）を行います。これにより最近傍法での分類（ラベル付け）はトレーニング用データ（インスタンス）に大きく依存する傾向があるという特徴があります。

なお、本ページで利用しているデータならびにコードはサンプルファイルをベースにしています。また、【】で表記されているページ数は書籍『Rによる機械学習（第2刷）』に基づいています。

R Packages

テキストで利用しているパッケージは“Mandatory”のパッケージのみですが、本ページでは“Optional”のパッケージも利用しています。また、tidymodelsならびにtidyverseパッケージはモダンなRの機械学習プログラミングでは必須のパッケージです。

Package		Descriptions
class	Mandatory	Functions for Classification
gmodels	Mandatory	Various R Programming Tools for Model Fitting
caret	Optional	Classification and Regression Training
e1071	Optional	Misc Functions of the Department of Statistics, Probability Theory Group (Formerly: E1071), TU Wien
skimr	Optional	Compact and Flexible Summaries of Data
tidymodels	N/A	Easily Install and Load the ‘Tidymodels’ Packages
tidyverse	N/A	Easily Install and Load the ‘Tidyverse’

3.1 最近傍法による分類とは何か【P60】

最近傍法とはラベルのついたトレーニングデータを用いてラベルのないデータをラベリングする方法です。

k近傍法のアルゴリズム【P60】

k近傍法（k-nearest neighbor algorithm, k-NN）は、分類（判別、予測、クラス分け、ラベル付け）したいデータの近傍にあるk個のトレーニング（学習）データを用いて分類を行うアルゴリズムです。乱暴にいうと

分類したいデータの近傍にあるk個のトレーニングデータによる多数決

みたいなイメージです。つまり、k近傍法を使うためには対象インスタンスとインスタンスの2点間の距離、一般的にはユークリッド距離（L2距離）を計算するためのデータ（個々のインスタンスの特徴を表す数値データ（順序尺度、間隔尺度、比例尺度））と分類するためのラベルデータ（名義尺度）が必要になります。

ユークリッド距離はn次元の直交座標系であれば計算が可能ですので、主成分分析のような多変量（多変数）のフィーチャーを持つインスタンス（観測単位の具体例）を分類するのに使え、その特徴は以下の通りです。

【表3−1】より

長所

単純で効果的
トレーニングデータの分布に前提条件がない
- 分類境界が不規則な場合に効果を発揮することが多い
トレーニングが高速

短所

モデルを作らないので結果の理解が難しい
- アルゴリズム自体が単純なので説明しやすいという主張もある
kの値によって結果が変わることがある
データが多いとトレーニング後の分類処理に時間がかかる
- 距離を総当たり（Brute Force）で計算するため
- 高速に計算する方法が色々と研究・実装されている（FNNパッケージなど）
名義フィーチャー（変数）と欠損値に対する処理が必要

　
短所もありますが分類系の問題には概ね適用でき、レコメンド系（おすゝめ、サジェスト）では様々な業種で活用されているようです。アルゴリズムとしてのk近傍法の選択基準は Choosing the right estimator などで紹介されています。

距離による類似性の測定【P62】

前述のようにk近傍法はユークリッド距離（\(L_2\)距離）を用いてテスト用インスタンスの近傍にあるk個のトレーニング用インスタンスを探し、多数決によりどのラベルにするかを計算します。n次元の直交空間における二つのインスタンス（P, Q）間のユークリッド距離（\(L_2\)距離）\(d_2(P, Q)\)は

\[d_2(P, Q) = \sqrt{(P_1 - Q_1)^2 + (P_2 - Q_2)^2 + ... + (P_n - Q_n)^2} \] \[= \sqrt{\sum_{i=1}^{n}(P_i - Q_i)^2} = d_2(Q, P)\]

で与えられます。

マンハッタン距離（\(L_1\)距離）【テキスト外】

距離にはユークリッド距離（\(L_2\)距離）の他にマンハッタン距離（\(L_1\)距離）と呼ばれる距離があります。その計算方法は以下の通りです。

\[d_1(P, Q) = \sum_{i = 1}^{n}{|P_i - Q_1|} = d_1(Q, P)\]

ちなみにマンハッタン距離の名前はニューヨーク州のマンハッタン島のような升目状の道路を移動する際の距離に由来しているらしいです。他にもn次元における距離はマハラノビス距離、チェビシェフ距離、ミンコフスキー距離などもあります。

ミンコフスキー距離（\(L_n\)距離）【テキスト外】

ミンコフスキー距離（\(L_n\)）はユークリッド距離やマンハッタン距離を一般化した以下の式で定義される距離です。\(p = 1\)の場合はマンハッタン距離、\(p = 2\)の場合はユークリッド距離になります。

\[d_p(P, Q) = (\sum_{i = 1}^{n}|P_i - Q_i|^p)^{\frac{1}{p}}\]

重みづけを用いた類似性の測定【テキスト外】

k近傍法は距離の近いk個のトレーニングインスタンスのラベルを用いてテストインスタンスを分類しますので、距離自体は分類に用いていません（近いトレーニングデータを探すのに用いているだけです）。距離が近い方が類似性が高いと考えるのは当然で、そのような考え方に対応した「重みづけk近傍法（Modified or Weighted k-Nearest Neighbor algorithm」というアルゴリズムがあります。kknnパッケージを使うとミンコフスキー距離を用いた重みづけk近傍法が使えます。

最適なkの選択【P63】

kの値により汎化性能が変わるのはテキストに記載してある通りですが、実際にkの値を変えるとどのように分類が変わるでしょうか？それを確認できる K-Nearest Neighbors Demo というサイトがあります。kの値を偶数にすると白い領域が出てきますが、これは近傍の数の数が各ラベルで同数（タイ）になる領域です。このようなデモを見る限り奇数のkの値を採用する方が汎化性能が高いと言えます。
実際にkの値を求めるには交差検証を用いるのが一般的です。交差検証を行うにはe1071パッケージやcaretパッケージを用います。具体的な計算方法は後述します。

k近傍法で使うデータの準備【P65】

ユークリッド距離は前述のように各フィーチャの差の二乗和の平方根で与えられます。ですので、各フィーチャーが取る値の範囲が大きく異なると大きな範囲を持つフィーチャーにユークリッド距離が引っ張られてしまう点に注意が必要です。フィーチャーの範囲が一桁異なれば、ユークリッド距離も異なってしまいます。

例えば、x, y, zという三つのフィーチャーをもつ三つのインスタンス間のユークリッド距離を求めてみます。二つのデータセットの違いはyのフィーチャが取る値の範囲が一桁異なっている点です。

data.frame(x = c(1, 2, 3), y = c(4, 5, 6), z = c(7, 8, 9),
           rowname = c("A", "B", "C")) %>% 
  tibble::column_to_rownames()

data.frame(x = c(1, 2, 3), y = c(40, 50, 60), z = c(7, 8, 9),
           rowname = c("A", "B", "C")) %>% 
  tibble::column_to_rownames()

ユークリッド距離はdist関数で求められますが、引数がmatrix形式なのでデータフレーム型のデータを渡す場合は注意してください。

data.frame(x = c(1, 2, 3), y = c(4, 5, 6), z = c(7, 8, 9),
           rowname = c("A", "B", "C")) %>% 
  tibble::column_to_rownames() %>% 
  dist(diag = TRUE)

##          A        B        C
## A 0.000000                  
## B 1.732051 0.000000         
## C 3.464102 1.732051 0.000000

data.frame(x = c(1, 2, 3), y = c(40, 50, 60), z = c(7, 8, 9),
           rowname = c("A", "B", "C")) %>% 
  tibble::column_to_rownames() %>% 
  dist(diag = TRUE)

##          A        B        C
## A  0.00000                  
## B 10.09950  0.00000         
## C 20.19901 10.09950  0.00000

そこで、フィーチャの取る値の範囲が異なっている特定のフィーチャーの影響を少なくするための方法が正規化です。正規化の代表的な手法には以下の二つがあります。

最小最大正規化（min-max normalization）【P65】

最小最大正規化はフィーチャーのデータが\(0\)(zero)から\(1\)の間になるようにします。Rでは関数が用意されていませんので利用者が定義する必要があります。

\[x_{new} = \frac{x - min(x)}{max(x) - min(x)} = \frac{x - min(x)}{diff(range(x))}\]

Zスコア正規化（Z-score normalization）【P66】

Zスコア正規化は平均値が\(0\)、分散\(1\)の標準正規分布になるようにします。Rではscale関数が用意されています。

\[x_{new} = \frac{x - \mu_{x}}{\sigma_x} = \frac{x - mean(x)}{sd(x)} = scale(x)\]

scale関数の返り値は“atomic vector”ではなく属性付きのマトリクス型である点に点に注意してください。

scale(c(1:5)) %>% str()

##  num [1:5, 1] -1.265 -0.632 0 0.632 1.265
##  - attr(*, "scaled:center")= num 3
##  - attr(*, "scaled:scale")= num 1.58

最小最大正規化は単純ですが将来的に最小値、最大値の範囲を超えるデータが出てきて、それを分類しなければならない場合にはあまり好ましい方法とは言えません（機械学習的に表現すると汎化性能が低い）。一方、Zスコア正規化は将来的に平均値、標準偏差が大きく変わらないであろうという想定の元であれば最小最大正規化よりは好ましい方法です。

正規化の効果を確認する【テキスト外】

先程の二組のデータセットを正規化してユークリッド距離を求めてみると正規化の効果が分かると思います。

最小最大正規化

前述のように最小最大正規化の関数は用意されていませんので、定義しておく必要があります。

normalize <- function(x) {
  return((x - min(x)) / diff(range(x)))
}

data.frame(x = c(1, 2, 3), y = c(4, 5, 6), z = c(7, 8, 9),
           rowname = c("A", "B", "C")) %>% 
  dplyr::mutate_if(is.numeric, normalize) %>% 
  tibble::column_to_rownames() %>% 
  dist(diag = TRUE)

##           A         B         C
## A 0.0000000                    
## B 0.8660254 0.0000000          
## C 1.7320508 0.8660254 0.0000000

data.frame(x = c(1, 2, 3), y = c(40, 50, 60), z = c(7, 8, 9),
           rowname = c("A", "B", "C")) %>% 
  dplyr::mutate_if(is.numeric, normalize) %>% 
  tibble::column_to_rownames() %>% 
  dist(diag = TRUE)

##           A         B         C
## A 0.0000000                    
## B 0.8660254 0.0000000          
## C 1.7320508 0.8660254 0.0000000

Zスコア正規化

data.frame(x = c(1, 2, 3), y = c(4, 5, 6), z = c(7, 8, 9),
           rowname = c("A", "B", "C")) %>% 
  dplyr::mutate_if(is.numeric, scale) %>% 
  tibble::column_to_rownames() %>% 
  dist(diag = TRUE)

##          A        B        C
## A 0.000000                  
## B 1.732051 0.000000         
## C 3.464102 1.732051 0.000000

data.frame(x = c(1, 2, 3), y = c(40, 50, 60), z = c(7, 8, 9),
           rowname = c("A", "B", "C")) %>% 
  dplyr::mutate_if(is.numeric, scale) %>% 
  tibble::column_to_rownames() %>% 
  dist(diag = TRUE)

##          A        B        C
## A 0.000000                  
## B 1.732051 0.000000         
## C 3.464102 1.732051 0.000000

ダミーコーディング【P66】

数値データは前述のように正規化を用いることで適切な値に変換できますが、カテゴリカルデータ（名義データ）の場合はどのようにすればよいでしょうか？このような際に便利なのがダミーコーディングです。例えば、よくある性別データをダミーコーディングし正規化すると以下のようになります。

data.frame(sex = c("M", "F", "M", "F", "M", "M", "M", "F")) %>% 
  dplyr::mutate(male = dplyr::if_else(sex == "M", 1, 0),
                male_minmax = (male - min(male)) / diff(range(male)), 
                male_z = scale(male))

また、三つのカテゴリがあるカテゴリカルデータをダミーコーディングした場合は以下のようになります（正規化は省略）。

data.frame(x = c("Hot", "Hot", "Cold", "Hot", "Medium", "Hot", "Cold", "Cold")) %>% 
  dplyr::mutate(hot = dplyr::if_else(x == "Hot", 1, 0),
                cold = dplyr::if_else(x == "Cold", 1, 0))

このようにダミーコーディングを使うとカテゴリ数が\(n\)の場合、\(n - 1\)個のインジケータ（フィーチャー）を作れば済み、正規化する必要もありません。なお、カテゴリ間の差が等間隔である場合は、数値へ落とし込むこともできます。例えば、等間隔であるサイズの場合は以下の用に三つの値にして最小最大正規化すると分かりやすくなります。

data.frame(size = c("Large", "Large", "Small", "Large", "Medium",
                    "Large", "Small", "Small")) %>% 
  dplyr::mutate(size_new = dplyr::if_else(size == "Small", 0,
                                          dplyr::if_else(size == "Medium", 1, 2)),
                size_minmax = (size_new - min(size_new)) / diff(range(size_new)),
                size_z = scale(size_new))

k近傍法が遅延学習なのはなぜか【P67】

k近傍法（kNN）は抽象化と汎化を行わないアルゴリズムなので、第一章における定義には当てはまりませんが、インスタンスを用いたトレーニングは行います（教師がいる）のでノンパラメトリックなアプローチに分類されています。

最近傍回帰【テキスト外】

最初に最近傍法はラベリングデータが離散変数（名義変数）と説明しましたが、ラベリングデータが連続値の場合でも適用可能で、この場合、最近傍回帰（Nearest Neighbors Regression）と呼ばれます。

3.2 実例 - k近傍法を使った乳ガン診断【P68】

ステップ1 - データの収集【P68】

データは UC Irvineの機械学習リポジトリから入手したウィスコンシン州のがん検診データを用います。各フィーチャーが何を意味するかはテキストで確認してください。

ステップ2 - データの研究と準備【P69】

データの確認【P69-70】

対象データを要約すると32の変量（フィーチャー）と569の観測値（インスタンス）があり、欠損値はないことが分かります。各フィーチャーの取る値の範囲は大きく異なっていますので正規化が必要なことが分かります。

skimr::skim_to_wide(wbcd)

データの削除と変換【P70】

変量の内idは受診者の識別番号であり、診断結果のdiagnosisは因子型として扱った方が適切と思われますので、削除と変換処理を行います。因子型変数の処理にはforcatsパッケージが便利です。

wbcd %>% 
  dplyr::select(-id) %>% 
  dplyr::mutate(diagnosis = forcats::fct_inorder(diagnosis)) %>% 
  dplyr::mutate(diagnosis = forcats::fct_recode(diagnosis,
                                                Malignant = "M",
                                                Benign = "B"))

変換 - 数値データの正規化【P71】

次に全てのIDを除く全ての数値型変量（フィーチャー）を正規化します。

# 最小値を0、最大値を1とする正規化を行う(NAがないので`na.rm`はデフォルト)
normalize <- function(x) {
  return((x - min(x)) / (max(x) - min(x)))
  # こちらだと属性が付与されてしまうので今回は使わない
  # scale(x, center = min(x), scale = max(x) - min(x))
}

wbcd_n <- wbcd %>% dplyr::select(-id) %>% 
  dplyr::mutate(diagnosis = forcats::fct_inorder(diagnosis)) %>% 
  dplyr::mutate(diagnosis = forcats::fct_recode(diagnosis,
                                                Malignant = "M",
                                                Benign = "B")) %>% 
  dplyr::mutate_if(is.numeric, normalize)

wbcd_n %>% 
  dplyr::select_if(is.numeric) %>% 
  skimr::skim_to_wide()

正規化後は全ての数値型フィーチャーが0～1の範囲のデータになっていることが分かります。また、個々のデータは下表のようになります（分かりやすく通し番号を付与してあります）。

wbcd_n %>% tibble::rownames_to_column("No")

データの準備 - 訓練、テストデータセットの作成【P72】

後ろから100個のインスタンスをテスト用、残りをトレーニング用データとして分けます。このようにデータを二分割してトレーニングとテストを行う方法をホールドアウト法（またはテストサンプル法）といいます。一般的にホールドアウト法は交差検証とはみなされません。
　

トレーニング用データ

# トレーニング用データ
(wbcd_train <- wbcd_n %>% 
  tibble::rowid_to_column("No") %>% 
  dplyr::filter(No <= 469) %>%
  dplyr::select(-diagnosis) %>% 
  tibble::column_to_rownames("No"))

テスト用データ

# テスト用データ
(wbcd_test <- wbcd_n %>% 
  tibble::rowid_to_column("No") %>% 
  dplyr::filter(No > 469) %>% 
  dplyr::select(-diagnosis) %>% 
  tibble::column_to_rownames("No"))

dplyr::top_n関数を使う場合【テキスト外】

dplyr::top_n関数は単純に行番号でフィルタする関数でなく、対象データの最後のフィーチャーの値を用いてランキング（オーダリング）したデータから指定数だけ上位または下位からサンプリングする関数です。
dplyr::top_n関数を用いて行番号順にサンプリングしたい場合は以下のように行番号をフィーチャーにして明示的に指定してください。

wbcd_n %>% 
  tibble::rowid_to_column("No") %>% 
  dplyr::top_n(n = 100, wt = No)

ランダムサンプリングによるデータの作成【テキスト外】

対象データのIDを見る限りランダムサンプリングしたデータのようなのでトレーニングデータ、テスト用を作成するのに更にランダムサンプリングする必要はなさそうですが、ランダムサンプリングをしてトレーニング用、テスト用データを作成する場合にはrsampleパッケージが便利です。

# 指定した比率にしたがってランダムに分割データを作るので実行は一回のみなので
# トレーニング用、テスト用に二回実行してはいけない。結果は`.$in_id`に格納される
split <- wbcd_n %>% 
  rsample::initial_split(prop = 1 - 100/569)

split %>% 
  rsample::training()   # .$in_idに該当するデータを取り出す

split %>% 
  rsample::testing()    # .$in_idに該当しないデータを取り出す

　
同様の処理はdplyrパッケージだけでも実現可能です。こちらは比率だけでなく個数でも指定可能です。

(train <- wbcd_n %>% 
  dplyr::sample_n(469))      # 比率の場合は`dplyr::sample_frac`関数を用いる

(test <- wbcd_n %>% 
  dplyr::anti_join(train))   # `dplyr::anti_join`でトレーニング用データを除く

　
また、dplyrパッケージでは因子（クラス）毎に同数をサンプリングすることも可能です。

iris %>% 
  dplyr::group_by(Species) %>% 
  dplyr::sample_n(10)

ラベルの作成【P72】

class::knn関数を使う場合、トレーニング用、テスト用のラベルは必ず“atomic vector”でなければなりません。

# トレーニング用データのラベル
wbcd_train_labels <- wbcd_n %>% 
  tibble::rowid_to_column("No") %>% 
  dplyr::filter(No <= 469) %>% 
  dplyr::select(diagnosis)

# テスト用データのラベル（性能評価する場合にのみラベルが必要）
wbcd_test_labels <- wbcd_n %>% 
  tibble::rowid_to_column("No") %>% 
  dplyr::filter(No > 469) %>% 
  dplyr::select(diagnosis)

# ラベルはベクトル変数でなければならない
wbcd_train_labels <- wbcd_train_labels$diagnosis
wbcd_test_labels <- wbcd_test_labels$diagnosis

wbcd_train_labels

##   [1] Benign    Benign    Benign    Benign    Benign    Benign    Benign   
##   [8] Malignant Benign    Benign    Malignant Benign    Benign    Benign   
##  [15] Malignant Benign    Benign    Benign    Malignant Benign    Benign   
##  [22] Benign    Benign    Benign    Benign    Malignant Benign    Malignant
##  [29] Benign    Benign    Benign    Malignant Malignant Benign    Benign   
##  [36] Benign    Malignant Benign    Malignant Malignant Malignant Malignant
##  [43] Malignant Benign    Benign    Malignant Benign    Malignant Benign   
##  [50] Benign    Malignant Benign    Benign    Benign    Malignant Benign   
##  [57] Benign    Benign    Malignant Malignant Malignant Malignant Malignant
##  [64] Malignant Malignant Benign    Benign    Benign    Benign    Benign   
##  [71] Malignant Benign    Benign    Benign    Benign    Benign    Malignant
##  [78] Benign    Benign    Malignant Benign    Benign    Benign    Benign   
##  [85] Benign    Benign    Benign    Benign    Malignant Benign    Benign   
##  [92] Benign    Malignant Benign    Malignant Malignant Benign    Benign   
##  [99] Benign    Malignant Benign    Benign    Benign    Malignant Benign   
## [106] Benign    Benign    Benign    Benign    Benign    Benign    Benign   
## [113] Malignant Malignant Benign    Malignant Malignant Malignant Malignant
## [120] Benign    Benign    Malignant Benign    Malignant Benign    Benign   
## [127] Malignant Malignant Malignant Malignant Malignant Benign    Benign   
## [134] Malignant Benign    Malignant Benign    Benign    Malignant Benign   
## [141] Malignant Malignant Malignant Malignant Malignant Benign    Malignant
## [148] Benign    Benign    Benign    Benign    Benign    Benign    Benign   
## [155] Benign    Benign    Benign    Malignant Benign    Benign    Benign   
## [162] Benign    Benign    Benign    Malignant Malignant Benign    Malignant
## [169] Benign    Benign    Malignant Malignant Malignant Benign    Malignant
## [176] Benign    Malignant Benign    Malignant Benign    Benign    Malignant
## [183] Benign    Malignant Benign    Benign    Malignant Malignant Malignant
## [190] Benign    Malignant Benign    Benign    Malignant Malignant Malignant
## [197] Malignant Benign    Benign    Benign    Malignant Benign    Benign   
## [204] Benign    Benign    Malignant Benign    Malignant Benign    Malignant
## [211] Benign    Malignant Malignant Benign    Benign    Benign    Benign   
## [218] Benign    Malignant Malignant Benign    Benign    Malignant Benign   
## [225] Benign    Benign    Benign    Malignant Malignant Benign    Benign   
## [232] Benign    Benign    Malignant Benign    Benign    Malignant Benign   
## [239] Benign    Benign    Malignant Benign    Benign    Malignant Malignant
## [246] Benign    Benign    Benign    Benign    Benign    Benign    Malignant
## [253] Benign    Malignant Benign    Benign    Benign    Benign    Benign   
## [260] Benign    Benign    Benign    Malignant Benign    Malignant Malignant
## [267] Benign    Benign    Benign    Malignant Benign    Malignant Benign   
## [274] Benign    Malignant Malignant Benign    Malignant Benign    Benign   
## [281] Malignant Benign    Benign    Benign    Malignant Benign    Malignant
## [288] Malignant Malignant Benign    Benign    Benign    Malignant Benign   
## [295] Malignant Malignant Malignant Malignant Benign    Malignant Malignant
## [302] Benign    Benign    Malignant Malignant Malignant Malignant Benign   
## [309] Benign    Benign    Malignant Malignant Benign    Benign    Malignant
## [316] Benign    Malignant Malignant Benign    Benign    Benign    Malignant
## [323] Malignant Benign    Benign    Malignant Benign    Malignant Benign   
## [330] Malignant Benign    Benign    Benign    Benign    Malignant Benign   
## [337] Benign    Benign    Malignant Benign    Benign    Malignant Malignant
## [344] Benign    Malignant Benign    Benign    Benign    Malignant Benign   
## [351] Benign    Malignant Benign    Benign    Malignant Benign    Benign   
## [358] Benign    Malignant Benign    Malignant Malignant Benign    Benign   
## [365] Benign    Benign    Malignant Benign    Benign    Malignant Benign   
## [372] Benign    Benign    Benign    Benign    Benign    Benign    Benign   
## [379] Benign    Benign    Benign    Benign    Malignant Malignant Benign   
## [386] Benign    Malignant Benign    Malignant Benign    Malignant Benign   
## [393] Benign    Malignant Benign    Benign    Benign    Malignant Malignant
## [400] Benign    Benign    Benign    Malignant Malignant Benign    Malignant
## [407] Benign    Benign    Malignant Benign    Benign    Benign    Benign   
## [414] Benign    Benign    Malignant Benign    Benign    Malignant Malignant
## [421] Benign    Malignant Benign    Benign    Benign    Malignant Benign   
## [428] Benign    Benign    Malignant Malignant Malignant Benign    Malignant
## [435] Benign    Benign    Malignant Benign    Benign    Benign    Benign   
## [442] Benign    Malignant Benign    Malignant Benign    Benign    Benign   
## [449] Benign    Malignant Benign    Malignant Malignant Benign    Benign   
## [456] Benign    Benign    Malignant Benign    Benign    Malignant Malignant
## [463] Benign    Benign    Malignant Benign    Benign    Malignant Benign   
## Levels: Benign Malignant

wbcd_test_labels

##   [1] Benign    Benign    Benign    Benign    Malignant Benign    Malignant
##   [8] Benign    Malignant Benign    Malignant Benign    Malignant Malignant
##  [15] Benign    Benign    Malignant Benign    Malignant Benign    Malignant
##  [22] Malignant Malignant Malignant Benign    Benign    Benign    Benign   
##  [29] Malignant Malignant Malignant Malignant Malignant Malignant Benign   
##  [36] Benign    Benign    Benign    Benign    Malignant Malignant Benign   
##  [43] Malignant Malignant Benign    Malignant Malignant Malignant Malignant
##  [50] Malignant Benign    Benign    Benign    Malignant Benign    Benign   
##  [57] Benign    Benign    Malignant Benign    Benign    Benign    Benign   
##  [64] Benign    Malignant Malignant Benign    Benign    Benign    Benign   
##  [71] Benign    Malignant Benign    Benign    Malignant Malignant Benign   
##  [78] Benign    Benign    Benign    Benign    Benign    Benign    Malignant
##  [85] Benign    Benign    Malignant Benign    Benign    Benign    Benign   
##  [92] Malignant Benign    Benign    Benign    Benign    Benign    Malignant
##  [99] Benign    Malignant
## Levels: Benign Malignant

ステップ3 - データによるモデルの訓練【P73】

見出しに「モデル」とありますが、遅延学習ではモデルの作成は行われません。トレーニングデータを用いてテストデータのラベル付けを行うだけです。なお、kの値（最近傍の数）にはトレーニング用インスタンス数の平方根に近い整数（奇数）を指定しています。kの値を奇数にする理由は「“二項分類（二値分類）”の場合に同票数で分類できなくなる問題を避ける」（多数決でタイにならないようにする）ためです。

wbcd_test_pred <- class::knn(train = wbcd_train, test = wbcd_test,
                             cl = wbcd_train_labels, k = 21)

wbcd_test_pred

##   [1] Benign    Benign    Benign    Benign    Malignant Benign    Malignant
##   [8] Benign    Malignant Benign    Malignant Benign    Malignant Malignant
##  [15] Benign    Benign    Malignant Benign    Malignant Benign    Malignant
##  [22] Malignant Malignant Malignant Benign    Benign    Benign    Benign   
##  [29] Malignant Malignant Malignant Benign    Malignant Malignant Benign   
##  [36] Benign    Benign    Benign    Benign    Malignant Malignant Benign   
##  [43] Malignant Malignant Benign    Malignant Malignant Malignant Malignant
##  [50] Malignant Benign    Benign    Benign    Benign    Benign    Benign   
##  [57] Benign    Benign    Malignant Benign    Benign    Benign    Benign   
##  [64] Benign    Malignant Malignant Benign    Benign    Benign    Benign   
##  [71] Benign    Malignant Benign    Benign    Malignant Malignant Benign   
##  [78] Benign    Benign    Benign    Benign    Benign    Benign    Malignant
##  [85] Benign    Benign    Malignant Benign    Benign    Benign    Benign   
##  [92] Malignant Benign    Benign    Benign    Benign    Benign    Malignant
##  [99] Benign    Malignant
## Levels: Benign Malignant

ステップ4 - モデルの性能評価【P74】

分類ができましたので、クロス集計で性能を評価してみましょう。

gmodels::CrossTable(x = wbcd_test_labels, y = wbcd_test_pred,
                    prop.chisq = FALSE)

## 
##  
##    Cell Contents
## |-------------------------|
## |                       N |
## |           N / Row Total |
## |           N / Col Total |
## |         N / Table Total |
## |-------------------------|
## 
##  
## Total Observations in Table:  100 
## 
##  
##                  | wbcd_test_pred 
## wbcd_test_labels |    Benign | Malignant | Row Total | 
## -----------------|-----------|-----------|-----------|
##           Benign |        61 |         0 |        61 | 
##                  |     1.000 |     0.000 |     0.610 | 
##                  |     0.968 |     0.000 |           | 
##                  |     0.610 |     0.000 |           | 
## -----------------|-----------|-----------|-----------|
##        Malignant |         2 |        37 |        39 | 
##                  |     0.051 |     0.949 |     0.390 | 
##                  |     0.032 |     1.000 |           | 
##                  |     0.020 |     0.370 |           | 
## -----------------|-----------|-----------|-----------|
##     Column Total |        63 |        37 |       100 | 
##                  |     0.630 |     0.370 |           | 
## -----------------|-----------|-----------|-----------|
## 
##

ステップ5 - モデルの性能の改善【P76】

変換 - Zスコア標準化【P76】

汎化性能を確保するためにZスコア正規化を使った場合を確認しておきます。Zスコア正規化には前述のようにscale関数を用いますが、scale関数の返り値は“atomic vector”にならないので、purrr::map関数を用いてscale関数を適用します。

wbcd_nz <- wbcd %>% dplyr::select(-id) %>% 
  dplyr::mutate(diagnosis = forcats::fct_inorder(diagnosis)) %>% 
  dplyr::mutate(diagnosis = forcats::fct_recode(diagnosis,
                                                Malignant = "M",
                                                Benign = "B")) %>% 
  purrr::map_if(is.numeric, scale) %>% as.data.frame()
  # dplyr::mutate_if(is.numeric, scale, center = FALSE, scale = FALSE)

wbcd_nz %>% 
  dplyr::select_if(is.numeric) %>%
  skimr::skim_to_wide()

トレーニング用、テスト用データならびにラベルの作成【P77】

最小最大正規化と同様のトレーニング用、テスト用データを作成します。

split <- wbcd_nz %>% 
  rsample::initial_split(prop = 1 - 100/569)

wbcd_train_z <- split %>% 
  rsample::training()   # .$in_idに該当するデータを取り出す
wbcd_test_z <- split %>% 
  rsample::testing()    # .$in_idに該当しないデータを取り出す

wbcd_train_z_labels <- wbcd_train_z$diagnosis
wbcd_test_z_labels <- wbcd_test_z$diagnosis

wbcd_test_z_pred <- class::knn(train = wbcd_train_z[, -1],
                               test = wbcd_test_z[, -1],
                               cl = wbcd_train_z_labels, k = 21)

gmodels::CrossTable(x = wbcd_test_z_labels, y = wbcd_test_z_pred,
                    prop.chisq = FALSE)

## 
##  
##    Cell Contents
## |-------------------------|
## |                       N |
## |           N / Row Total |
## |           N / Col Total |
## |         N / Table Total |
## |-------------------------|
## 
##  
## Total Observations in Table:  100 
## 
##  
##                    | wbcd_test_z_pred 
## wbcd_test_z_labels |    Benign | Malignant | Row Total | 
## -------------------|-----------|-----------|-----------|
##             Benign |        69 |         1 |        70 | 
##                    |     0.986 |     0.014 |     0.700 | 
##                    |     0.972 |     0.034 |           | 
##                    |     0.690 |     0.010 |           | 
## -------------------|-----------|-----------|-----------|
##          Malignant |         2 |        28 |        30 | 
##                    |     0.067 |     0.933 |     0.300 | 
##                    |     0.028 |     0.966 |           | 
##                    |     0.020 |     0.280 |           | 
## -------------------|-----------|-----------|-----------|
##       Column Total |        71 |        29 |       100 | 
##                    |     0.710 |     0.290 |           | 
## -------------------|-----------|-----------|-----------|
## 
##

クロス集計はどちらにすべき？

テキストでは縦軸が“Predict”、横軸が“Actual”と指定しており、因子型の順番から良性（陰性）、悪性（陽性）の順になっています。

	予測（良性）	予測（悪性）	備考
実際（良性）	真陰性	偽陽性（FP）	陰性
実際（悪性）	偽陰性（FN）	真陽性	陽性

　
一方、偽陽性、偽陰性を説明するクロス集計表では以下のように縦軸が“Actual”、横軸が“Predict”になるように指定していることが多いようです。　

	疾患（あり）	疾患（なし）	備考
検査（陽性）	真陽性	偽陽性（FP）
検査（陰性）	偽陰性（FN）	真陰性

kの別の値【P77】

kの値を変えることで性能を変えることができるかも知れません。最小最大正規化したデータでkの値を変更（k = 1, 3, 5, 7, 9）した場合の結果を見てみましょう。

for (k in c(1, 3, 5, 7, 9)) {
  print(paste0("k = ", k))
  set.seed(seed)
  gmodels::CrossTable(x = wbcd_test_labels,
                      y = class::knn(train = wbcd_train, test = wbcd_test,
                                     cl = wbcd_train_labels, k = k),
                      prop.chisq = FALSE)
}

## [1] "k = 1"
## 
##  
##    Cell Contents
## |-------------------------|
## |                       N |
## |           N / Row Total |
## |           N / Col Total |
## |         N / Table Total |
## |-------------------------|
## 
##  
## Total Observations in Table:  100 
## 
##  
##                  | class::knn(train = wbcd_train, test = wbcd_test, cl = wbcd_train_labels,      k = k) 
## wbcd_test_labels |    Benign | Malignant | Row Total | 
## -----------------|-----------|-----------|-----------|
##           Benign |        58 |         3 |        61 | 
##                  |     0.951 |     0.049 |     0.610 | 
##                  |     0.983 |     0.073 |           | 
##                  |     0.580 |     0.030 |           | 
## -----------------|-----------|-----------|-----------|
##        Malignant |         1 |        38 |        39 | 
##                  |     0.026 |     0.974 |     0.390 | 
##                  |     0.017 |     0.927 |           | 
##                  |     0.010 |     0.380 |           | 
## -----------------|-----------|-----------|-----------|
##     Column Total |        59 |        41 |       100 | 
##                  |     0.590 |     0.410 |           | 
## -----------------|-----------|-----------|-----------|
## 
##  
## [1] "k = 3"
## 
##  
##    Cell Contents
## |-------------------------|
## |                       N |
## |           N / Row Total |
## |           N / Col Total |
## |         N / Table Total |
## |-------------------------|
## 
##  
## Total Observations in Table:  100 
## 
##  
##                  | class::knn(train = wbcd_train, test = wbcd_test, cl = wbcd_train_labels,      k = k) 
## wbcd_test_labels |    Benign | Malignant | Row Total | 
## -----------------|-----------|-----------|-----------|
##           Benign |        60 |         1 |        61 | 
##                  |     0.984 |     0.016 |     0.610 | 
##                  |     0.968 |     0.026 |           | 
##                  |     0.600 |     0.010 |           | 
## -----------------|-----------|-----------|-----------|
##        Malignant |         2 |        37 |        39 | 
##                  |     0.051 |     0.949 |     0.390 | 
##                  |     0.032 |     0.974 |           | 
##                  |     0.020 |     0.370 |           | 
## -----------------|-----------|-----------|-----------|
##     Column Total |        62 |        38 |       100 | 
##                  |     0.620 |     0.380 |           | 
## -----------------|-----------|-----------|-----------|
## 
##  
## [1] "k = 5"
## 
##  
##    Cell Contents
## |-------------------------|
## |                       N |
## |           N / Row Total |
## |           N / Col Total |
## |         N / Table Total |
## |-------------------------|
## 
##  
## Total Observations in Table:  100 
## 
##  
##                  | class::knn(train = wbcd_train, test = wbcd_test, cl = wbcd_train_labels,      k = k) 
## wbcd_test_labels |    Benign | Malignant | Row Total | 
## -----------------|-----------|-----------|-----------|
##           Benign |        61 |         0 |        61 | 
##                  |     1.000 |     0.000 |     0.610 | 
##                  |     0.968 |     0.000 |           | 
##                  |     0.610 |     0.000 |           | 
## -----------------|-----------|-----------|-----------|
##        Malignant |         2 |        37 |        39 | 
##                  |     0.051 |     0.949 |     0.390 | 
##                  |     0.032 |     1.000 |           | 
##                  |     0.020 |     0.370 |           | 
## -----------------|-----------|-----------|-----------|
##     Column Total |        63 |        37 |       100 | 
##                  |     0.630 |     0.370 |           | 
## -----------------|-----------|-----------|-----------|
## 
##  
## [1] "k = 7"
## 
##  
##    Cell Contents
## |-------------------------|
## |                       N |
## |           N / Row Total |
## |           N / Col Total |
## |         N / Table Total |
## |-------------------------|
## 
##  
## Total Observations in Table:  100 
## 
##  
##                  | class::knn(train = wbcd_train, test = wbcd_test, cl = wbcd_train_labels,      k = k) 
## wbcd_test_labels |    Benign | Malignant | Row Total | 
## -----------------|-----------|-----------|-----------|
##           Benign |        61 |         0 |        61 | 
##                  |     1.000 |     0.000 |     0.610 | 
##                  |     0.938 |     0.000 |           | 
##                  |     0.610 |     0.000 |           | 
## -----------------|-----------|-----------|-----------|
##        Malignant |         4 |        35 |        39 | 
##                  |     0.103 |     0.897 |     0.390 | 
##                  |     0.062 |     1.000 |           | 
##                  |     0.040 |     0.350 |           | 
## -----------------|-----------|-----------|-----------|
##     Column Total |        65 |        35 |       100 | 
##                  |     0.650 |     0.350 |           | 
## -----------------|-----------|-----------|-----------|
## 
##  
## [1] "k = 9"
## 
##  
##    Cell Contents
## |-------------------------|
## |                       N |
## |           N / Row Total |
## |           N / Col Total |
## |         N / Table Total |
## |-------------------------|
## 
##  
## Total Observations in Table:  100 
## 
##  
##                  | class::knn(train = wbcd_train, test = wbcd_test, cl = wbcd_train_labels,      k = k) 
## wbcd_test_labels |    Benign | Malignant | Row Total | 
## -----------------|-----------|-----------|-----------|
##           Benign |        61 |         0 |        61 | 
##                  |     1.000 |     0.000 |     0.610 | 
##                  |     0.938 |     0.000 |           | 
##                  |     0.610 |     0.000 |           | 
## -----------------|-----------|-----------|-----------|
##        Malignant |         4 |        35 |        39 | 
##                  |     0.103 |     0.897 |     0.390 | 
##                  |     0.062 |     1.000 |           | 
##                  |     0.040 |     0.350 |           | 
## -----------------|-----------|-----------|-----------|
##     Column Total |        65 |        35 |       100 | 
##                  |     0.650 |     0.350 |           | 
## -----------------|-----------|-----------|-----------|
## 
##

k	偽陰性(B/M)	偽陽性(M/B)	error rate
1	1	3	0.04
3	2	1	0.03
5	2	0	0.02
7	4	0	0.04
9	4	0	0.04

エラーレート（(偽陰性数 + 偽陽性数)/テスト数 \(= \frac{FN+FP}{FN+FP+TN+TP}\)）だけを見るとk = 5がベストですが、細胞の良性・悪性判断という分類の目的を考えると偽陰性（分類結果が良性であるが実際には悪性であるケース）を極力減らせる方向に振るべきだと考えられますのでk = 1が最適といえます。ただ、k = 1は最小値でありトレーニング用データに対してセンシティブ過ぎる可能性があり、判断が難しいところです。

交差検証【テキスト外】

交差検証（Cross Validation）とは分割したデータの一部でトレーニングを行い残るデータでテストを行いモデルの妥当性を検証（確認）する方法です。ホールドアウト法と異なるのは分割数分だけトレーニングとテストを繰り返し行う（交差させる）点です。そのためホールドアウト法に比べると時間がかかります。主な交差検証としては

leave-one-out交差検証（一個抜き交差検証）
k-fold交差検証（k分割交差検証）

があります。一般的に交差検証では正答率（\(= \frac{TP + TN}{TP+TN+FP+FN}\)）または誤答率（\(1 - 正答率\)）を指標としてモデルパラメータの最適値を求めます。k近傍法でkの値を選択するのにはこの交差検証を用いる方法が簡単です。しかし、交差検証を行ったからと言って、求められたkの値が分類目的に合っている保証はありません（例：テキストの事例では偽陰性（FN）が増えるのは好ましくないで単に正答率が高いk値では誤診招く可能性があります）。また、ランダムサンプリングを用いていますので全ての関数で結果が一致する保証はありません（本ページではランダム・シードを固定して再現性を確保できるようにしてはあります）。

kknnパッケージによる交差検証

kknn::train.kknn関数は“leave-one-out”（一個抜き）交差検証が行える関数です。文字通りデータから一個だけインスタンスを抜き出して、残るインスタンスでトレーニングを行い抜いたインスタンスでテストを行いエラーレート（誤答率\(= \ \frac{FP+FN}{TP+TN+FP+FN}\) = \(1 - 正答率\)）で評価します。これをインスタンスの個数分繰り返して最適なkの値を導き出します。したがって、かなりの計算時間を要します。

wbcd_train %>% 
  dplyr::mutate(.label = wbcd_train_labels) %>% 
  dplyr::select(.label, dplyr::everything()) %>% 
  kknn::train.kknn(.label ~ ., data = .)

## 
## Call:
## kknn::train.kknn(formula = .label ~ ., data = .)
## 
## Type of response variable: nominal
## Minimal misclassification: 0.02985075
## Best kernel: optimal
## Best k: 9

なお、kknnパッケージにはcv.kknn関数という“k-fold”（k-分割）交差検証を行う関数もありますが、使い方がよく分からないので割愛します。

e1071パッケージによる交差検証

e1071::tune.knn関数は“k-fold”（k-分割）交差検証が行える関数です。文字通りデータをk-分割し、一つをテスト用データ、残り（\(k - 1\)）をトレーニング用データとし、分割数（\(k\)）だけ繰り返しkknn::train.kknn関数と同様にエラーレート（誤答率）が最も少なくなるkの値を最適なkの値として返します。

set.seed(seed)
(knnfit <- e1071::tune.knn(x = wbcd_train, y = wbcd_train_labels, k = 1:30)) %>% 
  summary()

## 
## Parameter tuning of 'knn.wrapper':
## 
## - sampling method: 10-fold cross validation 
## 
## - best parameters:
##  k
##  7
## 
## - best performance: 0.03408881 
## 
## - Detailed performance results:
##     k      error dispersion
## 1   1 0.05328400 0.03783422
## 2   2 0.04680851 0.03139850
## 3   3 0.04685476 0.03584771
## 4   4 0.04042553 0.03539000
## 5   5 0.03834413 0.02972439
## 6   6 0.03621647 0.03014809
## 7   7 0.03408881 0.03354718
## 8   8 0.03834413 0.03723617
## 9   9 0.03408881 0.03354718
## 10 10 0.03626272 0.03625202
## 11 11 0.03621647 0.03479516
## 12 12 0.03834413 0.03585991
## 13 13 0.03834413 0.03856333
## 14 14 0.03834413 0.03293534
## 15 15 0.04047179 0.03536248
## 16 16 0.03617021 0.03623274
## 17 17 0.04047179 0.03536248
## 18 18 0.04259944 0.04132808
## 19 19 0.04472710 0.04186957
## 20 20 0.04472710 0.04186957
## 21 21 0.04472710 0.04186957
## 22 22 0.04685476 0.04107862
## 23 23 0.04685476 0.04107862
## 24 24 0.05111008 0.04391414
## 25 25 0.04898242 0.04374450
## 26 26 0.04898242 0.04374450
## 27 27 0.04685476 0.03983534
## 28 28 0.05111008 0.04391414
## 29 29 0.04898242 0.04374450
## 30 30 0.04685476 0.04460099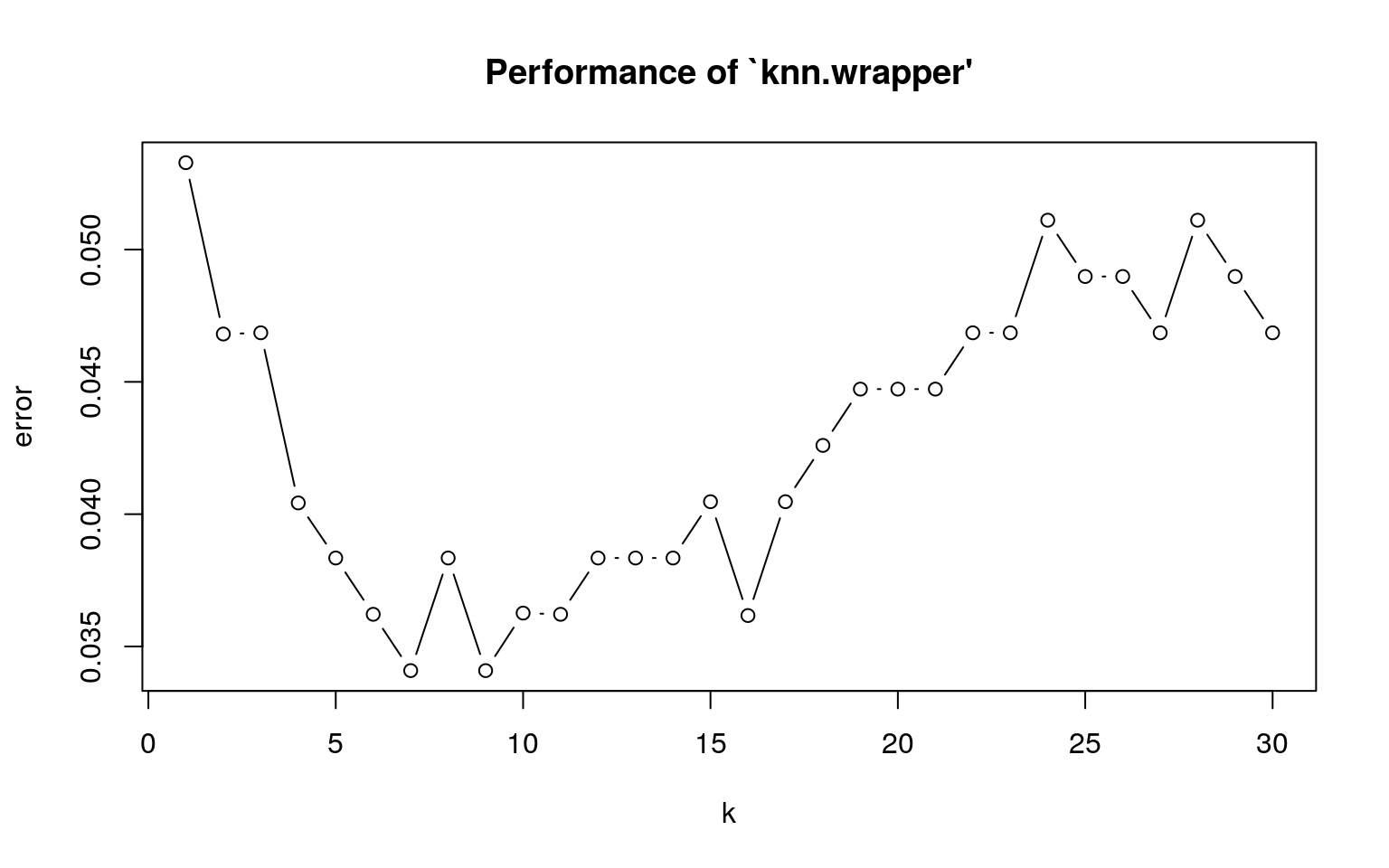

knnfit %>% 
  plot()

caretパッケージによる交差検証

caret::train関数は様々な交差検証を行える関数です。k近傍法の“k-fold”（k-分割）交差検証（デフォルトは10-fold）を行うには以下のように指定します。kの値の選択にはe1071::tune.knn関数などとは異なり“Accuracy”（正答率\(= \ \frac{TP+TN}{TP+TN+FP+FN}\)）が使われます。

set.seed(seed)
(knnfit <- caret::train(x = wbcd_train, y = wbcd_train_labels,
             method = "knn", tuneGrid = expand.grid(k = c(1:30)),
             trControl = caret::trainControl(method = "cv")))

## k-Nearest Neighbors 
## 
## 469 samples
##  30 predictor
##   2 classes: 'Benign', 'Malignant' 
## 
## No pre-processing
## Resampling: Cross-Validated (10 fold) 
## Summary of sample sizes: 422, 422, 422, 423, 422, 423, ... 
## Resampling results across tuning parameters:
## 
##   k   Accuracy   Kappa    
##    1  0.9531395  0.8993077
##    2  0.9424530  0.8765275
##    3  0.9638221  0.9215192
##    4  0.9595205  0.9124290
##    5  0.9593837  0.9119352
##    6  0.9636852  0.9213257
##    7  0.9722441  0.9398109
##    8  0.9701164  0.9352656
##    9  0.9721997  0.9397401
##   10  0.9722441  0.9398109
##   11  0.9722903  0.9397514
##   12  0.9658148  0.9257577
##   13  0.9679887  0.9302466
##   14  0.9701164  0.9349313
##   15  0.9701164  0.9346985
##   16  0.9680331  0.9299963
##   17  0.9659054  0.9253289
##   18  0.9615576  0.9158834
##   19  0.9593837  0.9109249
##   20  0.9637758  0.9206613
##   21  0.9594280  0.9110979
##   22  0.9573447  0.9068212
##   23  0.9529968  0.8972578
##   24  0.9571635  0.9061467
##   25  0.9572541  0.9062573
##   26  0.9573003  0.9065484
##   27  0.9551727  0.9019985
##   28  0.9508711  0.8923742
##   29  0.9530450  0.8973327
##   30  0.9530450  0.8973327
## 
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was k = 11.

可視化も簡単に行えます。

knnfit %>% 
  ggplot2::ggplot()

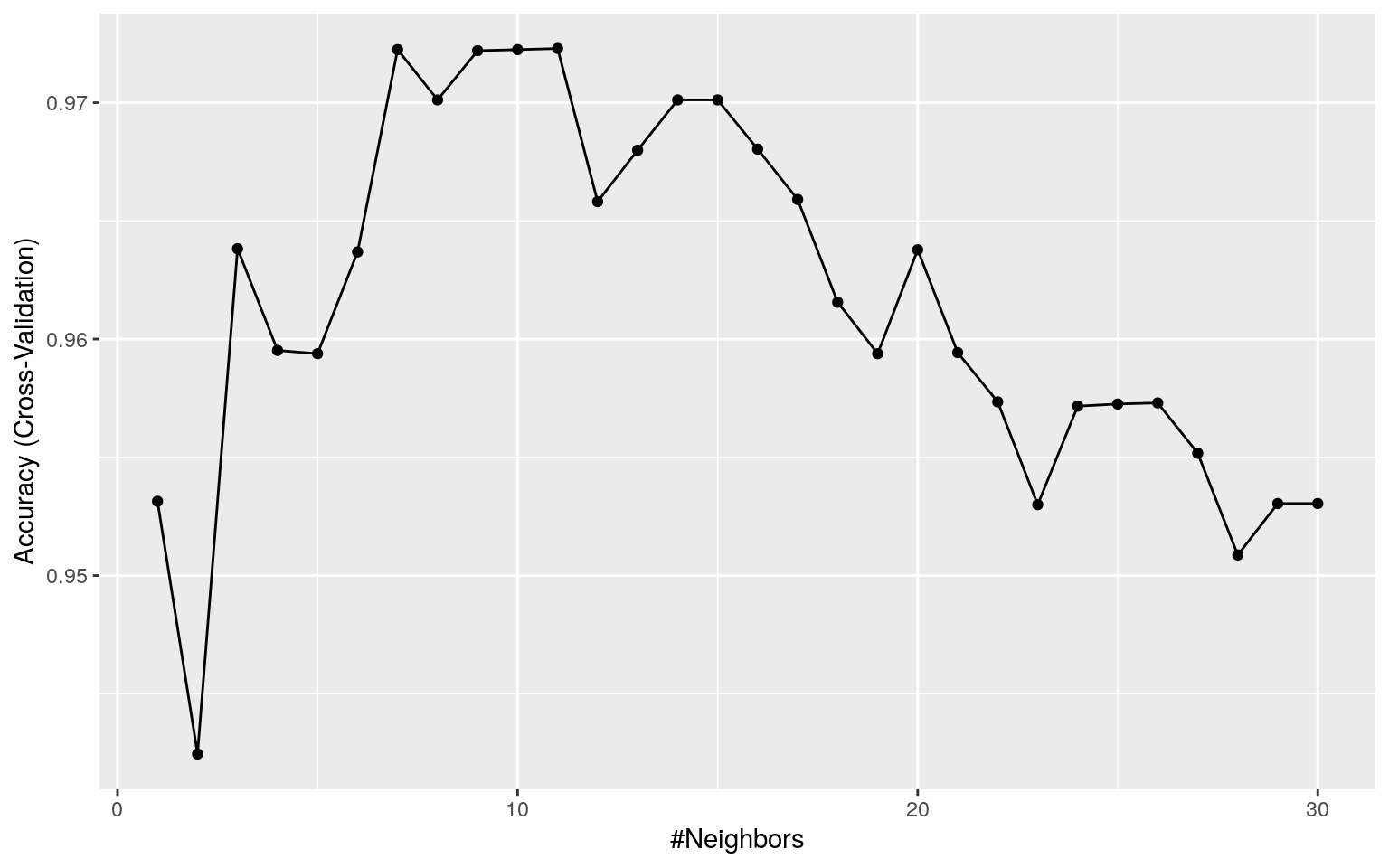
繰返し交差検証（上記の交差検証を指定回数繰り返して行う検証）を行うことや、fold数を変更することも可能な便利な関数です。

set.seed(seed)
caret::train(x = wbcd_train, y = wbcd_train_labels,
             method = "knn", tuneGrid = expand.grid(k = c(1:30)),
             trControl = caret::trainControl(method = "repeatedcv",
                                             number = 5, repeats = 5))

## k-Nearest Neighbors 
## 
## 469 samples
##  30 predictor
##   2 classes: 'Benign', 'Malignant' 
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold, repeated 5 times) 
## Summary of sample sizes: 374, 376, 375, 376, 375, 374, ... 
## Resampling results across tuning parameters:
## 
##   k   Accuracy   Kappa    
##    1  0.9522294  0.8968087
##    2  0.9556656  0.9039412
##    3  0.9637693  0.9211837
##    4  0.9612160  0.9157057
##    5  0.9641948  0.9221493
##    6  0.9641902  0.9222380
##    7  0.9693105  0.9332125
##    8  0.9671874  0.9285852
##    9  0.9684685  0.9314375
##   10  0.9684640  0.9313171
##   11  0.9705782  0.9357449
##   12  0.9667347  0.9272001
##   13  0.9667438  0.9273592
##   14  0.9671558  0.9281612
##   15  0.9641815  0.9214550
##   16  0.9607544  0.9139518
##   17  0.9586312  0.9094025
##   18  0.9594824  0.9111328
##   19  0.9577665  0.9073739
##   20  0.9564854  0.9044793
##   21  0.9560644  0.9034461
##   22  0.9547786  0.9006826
##   23  0.9556343  0.9025663
##   24  0.9552178  0.9016661
##   25  0.9535064  0.8978661
##   26  0.9513696  0.8932845
##   27  0.9522253  0.8951868
##   28  0.9526554  0.8960409
##   29  0.9535064  0.8978962
##   30  0.9535064  0.8978962
## 
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was k = 11.

3.3 まとめ【P78】

k近傍法は分類結果しか出てこない（モデルを作らない）ので学習とは言い難い点はありますが、トレーニング用データと数行のコードでかなり正確な分類を行ってくれる便利なアルゴリズムであることが分かりました。ただし、分類結果はトレーニング用データに大きく左右される点、kの値の選択方法はこれが正解という唯一無二の解がない点には注意が必要です。また、様々なパッケージで様々な実装が行われていますので、目的や使い勝手にあったパッケージを選択する必要があります。

モデルの評価方法には正答率（\(Accuracy = \frac{TP+TN}{TP+TN+FP+FN} = 1 - \frac{FP+FN}{TP+TN+FP+FN}\)）の他に適合率（\(Precision = \frac{TP}{TP+FP}\)）や再現率（\(Recall = \frac{TP}{TP+FN}\)）といった指標が使われます。モデルの目的にあった評価指標を選択する必要があります。

Case Study 【テキスト外】

テキスト以外のデータを用いたk近傍法のケーススタディをこちらにまとめてあります。

参考資料

Perv | Index | Next

CC BY-NC-SA 4.0 , Sampo Suzuki [2019-08-24(JST)]

第3章 遅延学習 - 最近傍法を使った分類

第3章 遅延学習 - 最近傍法を使った分類

R Packages

3.1 最近傍法による分類とは何か 【P60】

k近傍法のアルゴリズム 【P60】

距離による類似性の測定 【P62】

マンハッタン距離（\(L_1\)距離）【テキスト外】

ミンコフスキー距離（\(L_n\)距離） 【テキスト外】

重みづけを用いた類似性の測定【テキスト外】

最適なkの選択 【P63】

k近傍法で使うデータの準備 【P65】

最小最大正規化（min-max normalization） 【P65】

Zスコア正規化（Z-score normalization） 【P66】

正規化の効果を確認する 【テキスト外】

最小最大正規化

Zスコア正規化

ダミーコーディング 【P66】

k近傍法が遅延学習なのはなぜか 【P67】

最近傍回帰 【テキスト外】

3.2 実例 - k近傍法を使った乳ガン診断 【P68】

ステップ1 - データの収集 【P68】

ステップ2 - データの研究と準備 【P69】

データの確認 【P69-70】

データの削除と変換 【P70】

変換 - 数値データの正規化 【P71】

データの準備 - 訓練、テストデータセットの作成 【P72】

トレーニング用データ

テスト用データ

dplyr::top_n関数を使う場合 【テキスト外】

ランダムサンプリングによるデータの作成 【テキスト外】

ラベルの作成 【P72】

ステップ3 - データによるモデルの訓練 【P73】

ステップ4 - モデルの性能評価 【P74】

ステップ5 - モデルの性能の改善 【P76】

変換 - Zスコア標準化 【P76】

トレーニング用、テスト用データならびにラベルの作成 【P77】

kの別の値 【P77】

交差検証 【テキスト外】

kknnパッケージによる交差検証

e1071パッケージによる交差検証

caretパッケージによる交差検証

3.3 まとめ 【P78】

Case Study 【テキスト外】

参考資料

第3章遅延学習 - 最近傍法を使った分類

第3章遅延学習 - 最近傍法を使った分類

3.1 最近傍法による分類とは何か【P60】

k近傍法のアルゴリズム【P60】

距離による類似性の測定【P62】

ミンコフスキー距離（\(L_n\)距離）【テキスト外】

最適なkの選択【P63】

k近傍法で使うデータの準備【P65】

最小最大正規化（min-max normalization）【P65】

Zスコア正規化（Z-score normalization）【P66】

正規化の効果を確認する【テキスト外】

ダミーコーディング【P66】

k近傍法が遅延学習なのはなぜか【P67】

最近傍回帰【テキスト外】

3.2 実例 - k近傍法を使った乳ガン診断【P68】

ステップ1 - データの収集【P68】

ステップ2 - データの研究と準備【P69】

データの確認【P69-70】

データの削除と変換【P70】

変換 - 数値データの正規化【P71】

データの準備 - 訓練、テストデータセットの作成【P72】

dplyr::top_n関数を使う場合【テキスト外】

ランダムサンプリングによるデータの作成【テキスト外】

ラベルの作成【P72】

ステップ3 - データによるモデルの訓練【P73】

ステップ4 - モデルの性能評価【P74】

ステップ5 - モデルの性能の改善【P76】

変換 - Zスコア標準化【P76】

トレーニング用、テスト用データならびにラベルの作成【P77】

kの別の値【P77】

交差検証【テキスト外】

3.3 まとめ【P78】